Diode-Transistor Logic (DTL)

Diode-Transistor Logic, or DTL, refers to the technology for designing and fabricating digital circuits wherein logic gates employ both diodes and transistors. DTL offers better noise margins and greater fan-outs than RTL, but suffers from low speed, especially in comparison to TTL.

RTL allows the construction of NOR gates easily, but NAND gates are relatively more difficult to get from RTL. DTL, however, allows the construction of simple NAND gates from a single transistor, with the help of several diodes and resistors.

Figure 1 shows an example of an 3-input DTL NAND gate. It consists of a single transistor Q configured as an inverter, which is driven by a current that depends on the inputs to the three input diodes D1-D3.

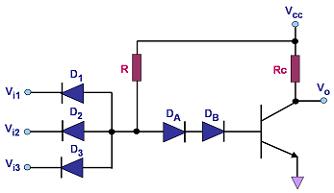Figure 1. A simple 3-input DTL NAND Gate

In the NAND gate in Figure 1, the current through diodes DA and DB will only be large enough to drive the transistor into saturation and bring the output voltage Vo to logic '0' if all the input diodes D1-D3 are 'off', which is true when the inputs to all of them are logic '1'. This is because when D1-D3 are not conducting, all the current from Vcc through R will go through DA and DB and into the base of the transistor, turning it on and pulling Vo to near ground.

However, if any of the diodes D1-D3 gets an input voltage of logic '0', it gets forward-biased and starts conducting. This conducting diode 'shunts' almost all the current away from the reverse-biased DA and DB, limiting the transistor base current. This forces the transistor to turn off, bringing up the output voltage Vo to logic '1'.

One advantage of DTL over RTL is its better noise margin. The noise margin of a logic gate for logic level '0', Δ0, is defined as the difference between the maximum input voltage that it will recognize as a '0' (Vil) and the maximum voltage that may be applied to it as a '0' (Vol of the driving gate connected to it). For logic level '1', the noise margin Δ1 is the difference between the minimum input voltage that may be applied to it as a '1' (Voh of the driving gate connected to it) and the minimum input voltage that it will recognize as a '1' (Vih).

Mathematically, Δ0 = Vil-Vol and Δ1 = Voh-Vih. Any noise that causes a noise margin to be overcome will result in a '0' being erroneously read as a '1' or vice versa. In other words, noise margin is a measure of the immunity of a gate from reading an input logic level incorrectly.

In a DTL circuit, the collector output of the driving transistor is separated from the base resistor of the driven transistor by several diodes. Circuit analysis would easily show that in such an arrangement, the differences between Vil and Vol, and between Voh and Vih, are much larger than those exhibited by RTL gates, wherein the collector of the driving transistor is directly connected to the base resistor of the driven transistor. This is why DTL gates are known to have better noise margins than RTL gates.

One problem that DTL doesn't solve is its low speed, especially when the transistor is being turned off. Turning off a saturated transistor in a DTL gate requires it to first pass through the active region before going into cut-off. Cut-off, however, will not be reached until the stored charge in its base has been removed. The dissipation of the base charge takes time if there is no available path from the base to ground. This is why some DTL circuits have a base resistor that's tied to ground, but even this requires some trade-offs. Another problem with turning off the DTL output transistor is the fact that the effective capacitance of the output needs to charge up through Rc before the output voltage rises to the final logic '1' level, which also consumes a relatively large amount of time. TTL, however, solves the speed problem of DTL elegantly.

See Also: TTL Parameters; Logic Gates; RTL; DTL; CMOS

HOME