Plotting Lognormal Distributions; Lognormal Plots

Plotting Lognormal Distributions

A life distribution is a collection of time-to-failure data, or life data, graphically presented as a plot of the number of failures versus time. It is just like any statistical distribution, except that the data involved are life data. The lognormal distribution is one of the most frequently used distributions in analyzing life or reliability data in the semiconductor industry.

The reason why semiconductor life data fit the lognormal distribution very well is because the lognormal distribution is formed by the multiplicative effects of random variables, and multiplicative interactions of variables are frequently encountered in many semiconductor failure mechanisms.

The lognormal life distribution is one wherein the natural logarithms of the lifetime data, ln(t), form a normal distribution. Consequently, the life data of a lognormal distribution will also form a straight line if plotted on a lognormal plot, i.e., a plot whose x- and y-axes stand for the cumulative % of failures and the logarithmic scale of time, respectively.

Life data are often analyzed on a per failure mechanism basis. Thus, an engineer who wishes to study the tendency of a device to fail by electromigration will conduct accelerated electromigration testing on a set of samples to generate the device's life data with respect to electromigration, i.e., the individual lifetimes exhibited by the tested samples before they fail by electromigration.

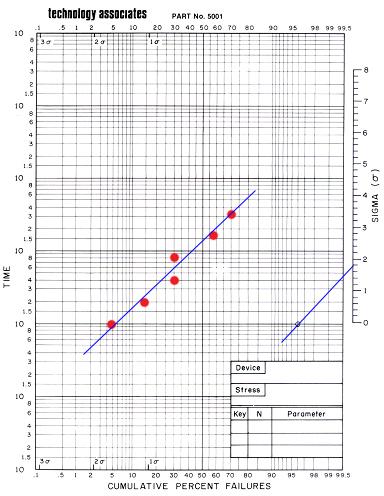
If one were to plot the cumulative % of failures corresponding to these life data against time on a lognormal plot, one would see that a straight line will emerge. Figure 1 shows an example of a lognormal plot.

Figure 1. An example of a lognormal plot using a lognormal

plotting sheet from Technology Associates

Basic guidelines for generating a lognormal plot include the following: 1) plot life data from a single failure mechanism only per plot; 2) use a data collection time interval that is in geometric progression so that the points will appear to be equally spaced in the log time scale; 3) plot all obtained data points, even those that reflect no additional failures and therefore resulting in the same cum % failures as the previous point; 4) plot actual data only - do not add unknown or unverified data; 5) draw an eyeball straight line through the data points, slightly giving more emphasis to data points near the media.

Once the plot has been created, one can estimate the median lifetime of the population by interpolating from the plot the time at which 50% of the failures would have occurred (in the example plot above, t50 is approximately at 150 hours). Also, an estimate, s, of the standard deviation (shape parameter) of the distribution may be obtained by drawing a line parallel to the distribution plot but passing through the bull's eye on the right side of the horizontal line t=10; s is where this line intersects the sigma nomograph on the right (in the example plot above, s is approximately 1.8). The ability to estimate cumulative percent failures from lognormal plots is an important tool in reliability assessments.

Primary Reference: D. S. Peck and O. D. Trapp, Accelerated Testing Handbook, Technology Associates.

Buy it now: Accelerated testing handbook

HOME